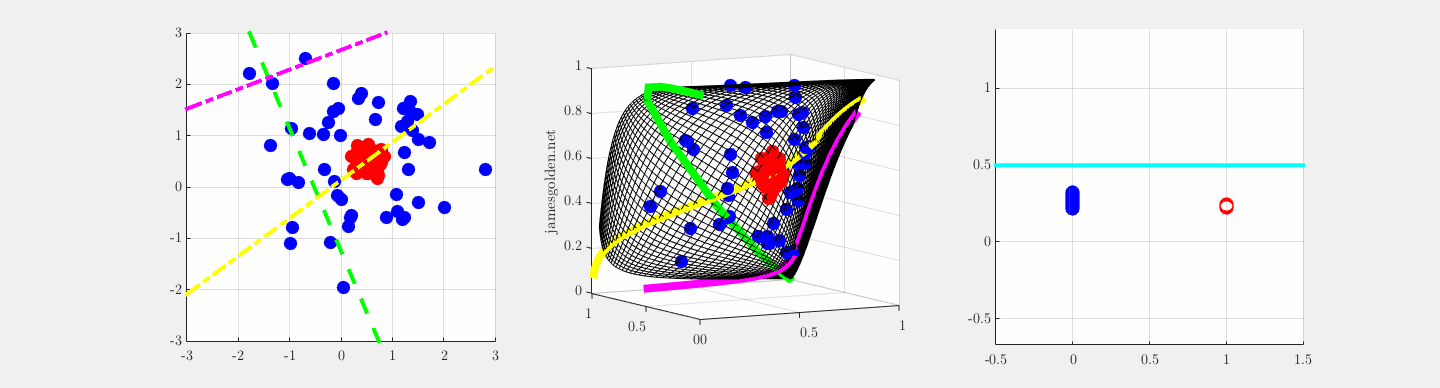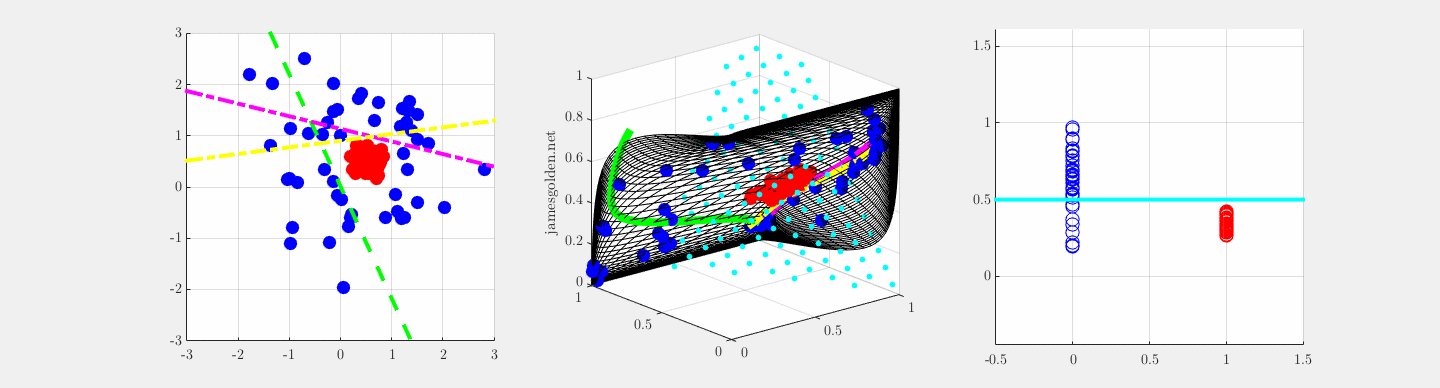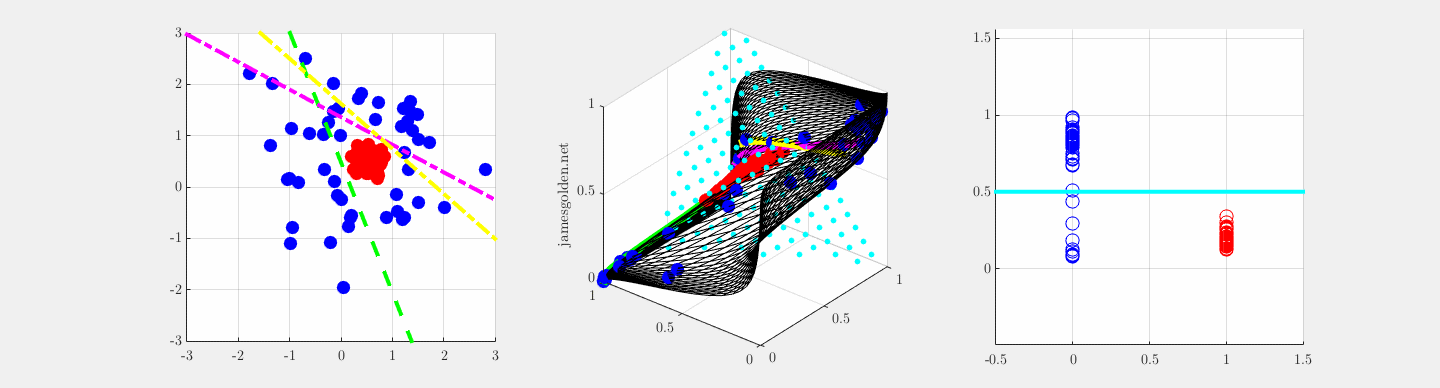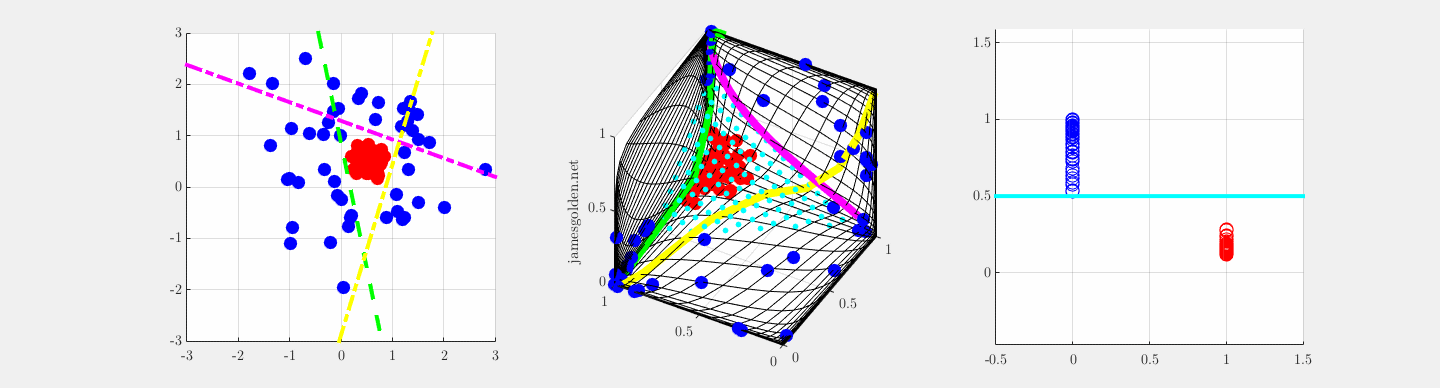
y = sig(W*x), z = sig(V*y) undergoing supervised training to separate blue and red, adapted from Olshausen, 2010.
“…Trained networks… contract space at the center of decision volumes and expand space in the vicinity of decision boundaries” – Nayebi & Ganguli, 2017
In order to correctly classify these data points in a 2D space as red or blue, a supervised two-layer network needs three feature vectors in the first layer (W; green, magenta and yellow) (Olah, 2014). If the projections onto those three feature vectors are plotted in a representation space where the features are orthogonal, we can observe how the network learns to warp the 2D input space lattice in 3D representation space in order to make classification possible with a single plane (blue cyan points), where projection onto a vector normal to the cyan plane separates the two classes (rightmost panel).
Learning feature vectors in W is equivalent to warping the input space within the representation space, and learning feature vector V is the placement of the separating plane (cyan points). Convolutional networks do something this in high dimensions to classify images, and measurements of the local curvature of the input space reveal how individual neurons and layers contribute to successful recognition.
The network is described by these equations for the two layers: y = sig(W*x), z = sig(V*y), where sig is a sigmoid nonlinearity.
Papers:
Golden, J. R., Vilankar, K. P., Wu, M. C., & Field, D. J. (2016). Conjectures regarding the nonlinear geometry of visual neurons. Vision research, 120, 74-92. (supplement)
Field, DJ, Golden, JR, Hayes, AJ. (2014). Contour Integration and the Association Field. In JS Werner, LM Chalupa (Eds.), The New Visual Neurosciences. Cambridge: The MIT Press [ToC].
G Menda, PS Shamble, EI Nitzany, JR Golden, RR Hoy. (2014). Visual Perception in the Brain of a Jumping Spider. Current Biology. NY Times (w/ autoplay video)
Contact: email (minus ‘invalid’) google scholar